The ‘use’ Macro in Elixir.

How to Use ‘use’ and ‘__using__’ Usefully In Your Modules.

Information on ‘use’ is Hard to Find.

I found learning ‘use’ unintuitive. Partially because I think it’s hard to find documentation for.

• ‘use’ is not searchable: Google searching “how to use ‘use’ in elixir” doesn’t return much information.
• ‘use’ is hidden in the elixir documentation: It’s in the Elixir documentation for alias, require, and import.
• There is no example for __using__ in a module: The elixir documentation states that ‘use’ calls the __using__ callback, but there’s no example implementation of this callback.

Also not trying to bash elixir documentation, the docs are fantastic. ❤

So What Is ‘use’?

here’s a lightweight explanation of ‘use’ in elixir as I currently understand it.

• Use is a tool to reuse code just like require, import, and alias.
• Use simply calls the __using__ macro defined in another module.
• The __using__ macro allows you to inject code into another module.

You can define a module with the __using__ macro and any code inside of the quote block will be injected into the module. like so:

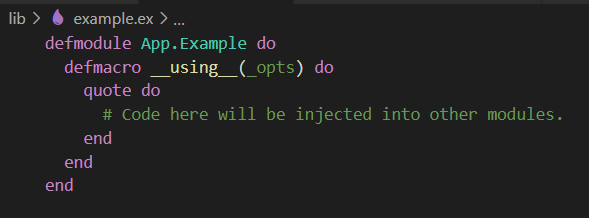
The quote block allows you to inject code to be evaluated at The app can then ‘use’ the Example module.

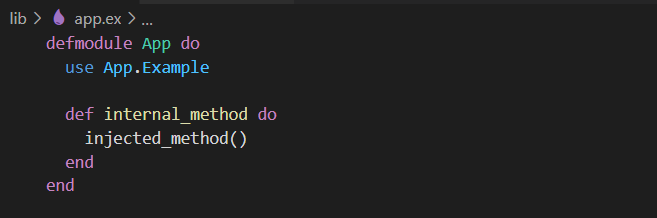
Code inside the __using__ module is injected into App. So if you define a function inside of the quote block:

Now the injected function can be used inside of the App module.

Why ‘use’ Instead of Import?

Looking at the above example, you might wonder why you should use ‘use’ instead of import. Import allows you to import all of the functions from a module, so you could accomplish the same goal like so:

However, ‘use’ allows you to inject more than just functions, you can also inject other alias’s, imports, and even inject other ‘use’ modules.

Now the InjectedAlias module can be used in the App module.

Use Allows You to Create Templates.

Have a common pattern? use allows you to codify the pattern into a template for making other modules.

Use is powerful and dangerous. It’s great when you have a reusable pattern you want to abstract away in your codebase. However, its strength is also its weakness. If you overuse the ‘use’ macro, you might hide too much of the complexity of your system and make it difficult to understand.

How Phoenix Leverages ‘use’.

Phoenix is a powerful example of how to leverage ‘use.’

Phoenix has common patterns. These patterns are provided out of the box in any phoenix application and include controllers, views, live views, channels, and more. If you aren’t familiar with Phoenix, that’s ok. It’s enough to know these are common patterns in a phoenix application.

These are all templates you can leverage to make routers, controllers, views, etc.

Nothing in code is magic, and all of the code to power these templates is in your application.

Phoenix applications have a Web module. It’s typically named <appname>Web, so I will generically refer to it as the Web module.

The Web module in your phoenix application leverages the __using__ macro.
with atoms passed in to inject the functionality for the different templates for :controller, :live_view, :view. :router etc.

So when you create a new router like so:

You inject the code from the Web module’s __using__ macro, which calls the router function in the Web module:

This quote block injects the code inside of it to call the Phoenix.Router module’s __using__ macro and inject the functionality for a Phoenix Router. That’s a 1000+ line file, so I won’t paste it in, but you can check out the Phoenix.Router module in your phoenix application if you are curious.

From start to finish, here’s a diagram to help you understand.

You don’t need to understand how phoenix applications leverage ‘use’ to create controllers, channels, views, etc. However, by including a more complex use case, I hope you can see the power of the ‘use’ macro.

Summary

Anytime you have a common pattern you want to repeat for modules, you can consider ‘use.’ For other cases, you should consider sticking with alias, require, and import. However, be cautious not to overuse the ‘use’ macro because it can hide functionality and behavior.

Use ‘use’ usefully by using __using__.

I’m sorry I had to sneak in one more.